Logo OFPPT

ISMO - Institut Spécialisé Dans les Métiers de l'Offshoring de Tétouan

Office de la Formation Professionnelle et de la Promotion du Travail

Introduction à l'Algorithmique et aux Structures de Données

Dernière mise à jour : Octobre 2025

Photo de P. Rahmouni Oussama

Par P. Rahmouni Oussama

Formateur en Développement Informatique & Data Science, ISMO

Parcours d'apprentissage

Modules à venir

  • Algorithmes de tri et de recherche
  • Introduction à la complexité algorithmique
  • Structures de données avancées (listes, piles, files)

Partie 1 : Les Fondations

Chapitre 1 : Qu'est-ce qu'un algorithme ?

Bienvenue dans le monde de l'algorithmique ! Ce cours est votre première étape pour apprendre à "penser comme un programmeur". Avant d'écrire du code dans un langage spécifique, il faut apprendre à structurer sa pensée pour résoudre des problèmes de manière logique et efficace. C'est exactement le rôle de l'algorithmique.

Définition : Algorithme

Un algorithme est une suite finie d'opérations ou de règles logiques destinées à résoudre un problème ou à accomplir une tâche, en partant d'une entrée pour aboutir à une sortie. Il peut être simple, comme une recette de cuisine, ou très complexe, comme ceux utilisés par Google pour classer les résultats de recherche.

Définition : Problème

En informatique, un problème n'est pas une difficulté, mais une tâche à accomplir. Il se définit par un objectif à atteindre à partir de données fournies en entrée. Par exemple, "calculer la moyenne de trois nombres" est un problème où les entrées sont les trois nombres et la sortie est leur moyenne.

↑ Retour en haut

Chapitre 2 : Les Instructions de Base

Pour construire nos "recettes", nous avons besoin d'ingrédients de base. En algorithmique, ce sont les instructions qui nous permettent de manipuler des données.

La Déclaration de Variables

Une variable est une "boîte" nommée qui stocke une information. Avant de l'utiliser, il faut la déclarer en précisant son nom et son type (entier, réel, chaîne de caractères, etc.). Cela permet à l'ordinateur de réserver l'espace mémoire nécessaire.

Variables
nom : chaine_de_caractères(30)
age : entier
prix : réel

L'Affectation

L'affectation est l'opération qui consiste à mettre une valeur dans une variable. On utilise souvent le symbole <-- pour la représenter.

age <-- 25
prix <-- 19.99
nom <-- "Alice"

La Lecture et l'Écriture (Entrée/Sortie)

Pour interagir avec l'utilisateur, on utilise deux instructions fondamentales :

  • Ecrire() : Pour afficher un message ou le contenu d'une variable à l'écran.
  • Lire() : Pour attendre que l'utilisateur tape une valeur et la stocker dans une variable.
Algorithme exemple1
Variables
nom : chaine_de_caractères(30)
Début
Ecrire("Tapez votre nom : ")
Lire(nom)
Ecrire("Bonjour ", nom)
Fin.

Exercice : Addition de deux nombres

Écrire un algorithme qui demande à l'utilisateur de taper deux nombres entiers, puis qui calcule et affiche leur somme.

Algorithme Addition
Variables
a, b, r : entiers
Début
Ecrire("Tapez la valeur de A : ")
Lire(a)
Ecrire("Tapez la valeur de B : ")
Lire(b)
r <-- a + b
Ecrire("La somme de ", a, " et ", b, " est ", r)
Fin.

Exercice : Permutation de deux variables

Écrire un algorithme qui échange les valeurs de deux variables A et B en utilisant une troisième variable temporaire.

Algorithme permutation
Variables
a, b, c : entiers
Début
Ecrire("Tapez la valeur de A : ")
Lire(a)
Ecrire("Tapez la valeur de B : ")
Lire(b)

c <-- a       // on garde la valeur de a dans une variable temporaire
a <-- b       // on met b dans a
b <-- c       // on remet l’ancienne valeur de a dans b

Ecrire("Après permutation : ")
Ecrire("A = ", a)
Ecrire("B = ", b)
Fin.
↑ Retour en haut

Partie 2 : La Logique Conditionnelle

Chapitre 3 : Les Conditions (Si... Sinon)

Rarement un programme exécute les mêmes instructions tout le temps. Le plus souvent, il doit prendre des décisions en fonction de certaines conditions. L'instruction Si...Alors...Sinon est l'outil principal pour cela.

Elle évalue une condition qui peut être soit VRAI, soit FAUX. Si elle est VRAI, un bloc d'instructions est exécuté. Sinon (et c'est optionnel), un autre bloc d'instructions est exécuté.

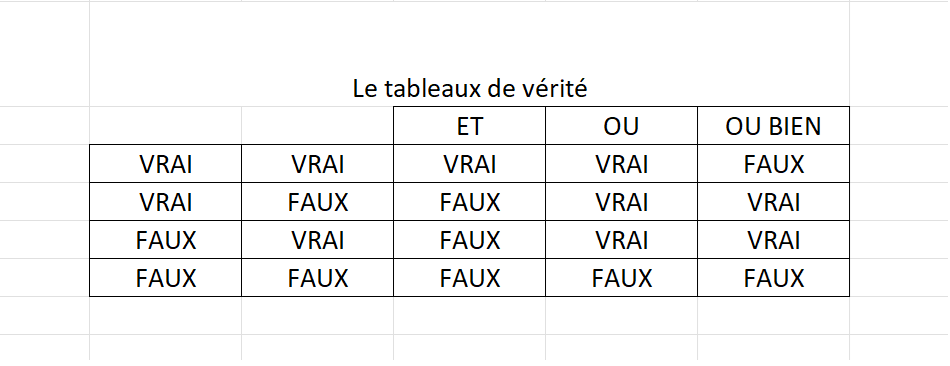
Conditions Combinées et Tableaux de Vérité

On peut combiner plusieurs conditions avec des opérateurs logiques comme ET et OU. Pour comprendre leur fonctionnement, on utilise les tableaux de vérité.

Tableau de vérité pour les opérateurs ET, OU, OU BIEN

Exercice : Salutation multilingue

Demander une langue (fr, ar, en, es) et le nom de l'utilisateur, puis le saluer dans la langue choisie.

Algorithme hello
Variables
nom, langue : chaine
Début
Ecrire("Choisissez une langue : fr, ar, en, es : ")
Lire(langue)
Ecrire("Tapez votre nom : ")
Lire(nom)

Si langue = "fr" alors
    Ecrire("Bonjour ", nom)
SinonSi langue = "ar" alors
    Ecrire("مرحبا ", nom)
SinonSi langue = "en" alors
    Ecrire("Hello ", nom)
SinonSi langue = "es" alors
    Ecrire("Hola ", nom)
Sinon
    Ecrire("Langue non reconnue !")
Fin Si
Fin.

Exercice : Le plus grand de trois entiers

Écrire un algorithme qui lit trois entiers (a, b, c) et affiche la plus grande valeur.

Méthode 1 : Conditions combinées
Si (a >= b) et (a >= c) alors 
Ecrire("La plus grande valeur est A")
SinonSi (b >= a) et (b >= c) alors
Ecrire("La plus grande valeur est B")
Sinon
Ecrire("La plus grande valeur est C")
Fin Si
Méthode 2 : Utilisation d’une variable max
Variables
a, b, c, max : entiers
Début
// ... Lecture de a, b, c ...
max <-- a
Si b > max alors
max <-- b
FinSi
Si c > max alors
max <-- c
Fin Si
Ecrire("La valeur maximale est ", max)
Fin.

Exercice : Équation du premier degré

Résoudre l’équation `a*x + b = 0`.

Si a <> 0 alors 
Ecrire("La solution est x = ", -b / a)
SinonSi b <> 0 alors
Ecrire("Aucune solution")
Sinon
Ecrire("Infinité de solutions")
FinSi

Exercice : Équation du second degré

Résoudre l'équation `a*x² + b*x + c = 0`.

Algorithme eq2deg
Variables
a, b, c, delta : réels
Début
// ... Lecture de a, b, c ...
Si a = 0 alors
// ... Traitement équation 1er degré ...
Sinon
delta <-- (bb) - (4ac)
Si delta < 0 alors
Ecrire("Aucune solution réelle")
SinonSi delta = 0 alors
Ecrire("Une solution double : x = ", -b / (2a))
Sinon
Ecrire("Deux solutions : ")
Ecrire("x1 = ", (-b - racine(delta)) / (2a))
Ecrire("x2 = ", (-b + racine(delta)) / (2a))
Fin Si
Fin Si
Fin.
↑ Retour en haut

Chapitre 4 : Le Choix Multiple (Selon Cas)

Quand une série de SinonSi devient trop longue et que toutes les conditions testent la même variable, il est plus propre et lisible d'utiliser l'instruction Selon...Cas. Elle évalue une variable et exécute le bloc de code correspondant à sa valeur.

Exercice : Jours de la semaine

Écrire un algorithme qui récupère le numéro d'un jour (1 à 7) et affiche son nom. Gérer les cas d'erreur.

ALGORITHME JoursSemaine
Variables
jour : ENTIER
DEBUT
Ecrire( "Tapez le jour de la semaine (1-7) : " )
Lire( jour )
Selon jour Faire
Cas 1 :
Ecrire( "Dimanche" )
Cas 2 :
Ecrire( "Lundi" )
Cas 3 :
Ecrire( "Mardi" )
Cas 4 :
Ecrire( "Mercredi" )
Cas 5 :
Ecrire( "Jeudi" )
Cas 6 :
Ecrire( "Vendredi" )
Cas 7 :
Ecrire( "Samedi" )
Cas Par Defaut :
Ecrire( "Erreur" )
Fin Selon
FIN

Exercice : Mention selon la note

Écrire un algorithme qui récupère une note sur 20 et affiche la mention correspondante (Excellent, Très Bien, etc.).

ALGORITHME Mentions
Variables
note : REEL
DEBUT
Ecrire( "Tapez votre note : " )
Lire( note )
Selon Faire
Cas note < 0 ou note > 20 :
Ecrire( "Invalide" )
Cas note < 10 :
Ecrire( "Insuffisant" )
Cas note < 12 :
Ecrire( "Passable" )
Cas note < 14 :
Ecrire( "Assez Bien" )
Cas note < 16 :
Ecrire( "Bien" )
Cas note < 18 :
Ecrire( "Très Bien" )
Cas note <= 20 :
Ecrire( "Excellent" )
Fin Selon
FIN
↑ Retour en haut

Partie 3 : Les Répétitions

Chapitre 5 : Les Boucles

Les boucles permettent d'exécuter un bloc d'instructions plusieurs fois. C'est un concept fondamental pour traiter des listes de données ou simplement pour répéter une action sans avoir à réécrire le même code.

La Boucle `Pour`

Utilisée quand on connaît à l'avance le nombre exact de répétitions. Elle utilise un "compteur" qui s'incrémente (ou se décrémente) à chaque tour.

Pour i allant de 1 à 10 Faire
Ecrire(i)
Fin Pour

La Boucle `Tant Que`

Répète un bloc d'instructions tant qu'une condition est vraie. La condition est vérifiée au début : si elle est fausse dès le départ, le bloc n'est jamais exécuté.

i <-- 1
Tant Que i <= 10 Faire
Ecrire(i)
i <-- i + 1
Fin Tant Que

La Boucle `Répéter... Jusqu'à`

Similaire à `Tant Que`, mais la condition est vérifiée à la fin. Cela garantit que le bloc d'instructions est exécuté au moins une fois.

i <-- 1
Répéter
Ecrire(i)
i <-- i + 1
Jusqu'à i > 10

Exercice : Table de multiplication

Écrire un algorithme qui lit un entier et affiche sa table de multiplication de 1 à 10.

pour i de 1 à 10 pas 1 faire
Ecrire( n, " x ", i, " = ", (n*i) )
fin pour

Exercice : Calculs sur une série de nombres

Écrire un algorithme qui demande à l'utilisateur de taper plusieurs entiers positifs, et s'arrête lorsqu'un nombre négatif est entré. Le programme doit alors afficher la somme, la moyenne, le plus grand et le plus petit des nombres positifs saisis.

ALGORITHME Principal
Variables
n, min, max, som, i : ENTIER
moy : REEL
DEBUT
i <-- 0
som <-- 0
Répéter
Ecrire( "Tapez une valeur (négative pour arrêter) : ")
Lire( n )
Si n >= 0 Alors
Si i = 0 Alors // Premier nombre positif
min <-- n
max <-- n
Sinon
Si n > max Alors
max <-- n
FinSi
Si n < min Alors
min <-- n
FinSi
Fin Si
som <-- som + n
i <-- i + 1
Fin Si
Jusqu'à n < 0

Si i > 0 Alors
    Ecrire( "La somme est ", som )
    moy <-- som / i
    Ecrire( "La moyenne est ", moy )
    Ecrire( "La plus grande valeur est ", max )
    Ecrire( "La plus petite valeur est ", min )
Sinon
    Ecrire("Aucun nombre positif n'a été entré.")
FinSi
FIN
↑ Retour en haut

Partie 4 : Les Structures de Données

Chapitre 6 : Les Tableaux

Imaginez devoir stocker 100 notes. Déclarer 100 variables serait fastidieux ! Un tableau est une structure qui permet de stocker plusieurs valeurs du même type dans une seule variable, accessible via un index (généralement à partir de 0).

Déclaration et Manipulation

Variables
// Déclare un tableau 't' de 3 entiers (indices 0, 1, 2)
t : TABLEAU de ENTIER
DEBUT
// Affecte la valeur 10 à la première case (index 0)
t <-- 10
t <-- 5

// Affiche le contenu de la deuxième case
Ecrire(t) // Affiche 5
FIN

Exercice : Afficher un tableau à l'envers

Écrire un algorithme qui demande à l'utilisateur de taper 5 entiers, les stocke dans un tableau, puis les réaffiche dans l'ordre inverse de la saisie.

ALGORITHME Principal
Variables
t : TABLEAU de ENTIER
i : ENTIER
DEBUT
Pour i allant de 0 à 4 Faire
Ecrire( "Tapez la valeur numéro ", (i+1) , " : ")
Lire( t[i] )
Fin Pour
Ecrire("Affichage à l'envers : ")
Pour i allant de 4 à 0 Pas -1 Faire
Ecrire( t[i] )
Fin Pour
FIN

Exercice : Recherche dans un tableau

Demander à l'utilisateur de remplir un tableau de 10 entiers. Ensuite, lui demander un nombre à chercher et indiquer si ce nombre existe dans le tableau et, si oui, à quelle position.

Exercice de Validation (Synthèse)

Écrire un algorithme complet qui calcule le montant final à payer par un client selon plusieurs critères (type de produit, montant, carte de fidélité). Cet exercice combine conditions, opérateurs logiques et calculs.

ALGORITHME CalculMontantFinal
Variables
nom_client, type_produit, reponse_carte : CHAINE
montant_achat, montant_final : REEL
a_carte_fidelite : BOOLEEN
DEBUT
// ... Lecture des données ...

// Appliquer la réduction de base
Selon type_produit Faire
    Cas "alimentaire": montant_final <-- montant_achat * 0.95
    Cas "habillement": montant_final <-- montant_achat * 0.90
    Cas "electronique": montant_final <-- montant_achat * 0.85
    Cas Par Defaut: montant_final <-- montant_achat
Fin Selon

// Appliquer la réduction de fidélité
Si a_carte_fidelite = vrai Alors
    montant_final <-- montant_final * 0.95
Fin Si

// Appliquer la remise spéciale
Si montant_final > 2000 Alors
    montant_final <-- montant_final * 0.97
Fin Si

Ecrire("Le montant final à payer est : ", montant_final, " dh")
FIN
↑ Retour en haut